| .vscode | ||
| assets | ||
| docs | ||
| include | ||
| macro | ||
| src | ||
| utils | ||
| .clang-format | ||
| .gitignore | ||
| CMakeLists.txt | ||
| debug.txt | ||
| G4.code-workspace | ||
| main.cpp | ||
| README.md | ||
| requirements.txt | ||
| vis.mac | ||
DESCSS
Dose Estimation by Simulation of China Space Station
中国空间站模拟剂量评估
空间辐射环境
轨道
- 空间站轨道根数(
TLE,2022.05.11)1
1 48274U 21035A 22131.00000000 .00018566 00000-0 21317-3 0 9998
2 48274 41.4696 84.9802 0011517 308.1456 44.4159 15.61130380 58963
| 偏心率 | 倾角 deg |
升交点赤经 deg |
近地点辐角 deg |
平近点角 deg |
|---|---|---|---|---|
| 0.001152 | 41.4696 | 84.9802 | 308.1456 | 44.4159 |
-
轨道参数
平近点角$M$与偏近点角$E$满足:$ M = E - e\cdot\sin{E}真近点角$T$与偏近点角$E$满足:$ \tan{\frac{T}{2}}=\sqrt{\frac{1+e}{1-e}}\tan{\frac{E}{2}}由此有:近地点
km远地点
km倾角
deg升交点赤经
deg近地点辐角
deg偏近点角
deg真近点角
deg379.2 393.8 41.4696 84.9802 308.1456 44.4167 44.4629 -
生成轨道
使用SPENVIS的Coordinate generators生成预计轨道,总计30天,保存为assets/orbit.csv文件。
辐射环境
银河宇宙射线2
银河宇宙射线 (GCR,Galactic cosmic rays) 是从系外进入太阳系的高能带电粒子,其通量与太阳活动负相关,主要由质子、电子和完全电离的原子核组成,核成分约占$98%$,分别为H($\approx87%$)、He($\approx12%$)和少量较重的原子核($\approx1%$)。
GCR一般各向同性,通量约为$1\sim10\ \mathrm{cm^{-2}s^{−1}}$,以高能粒子为主(可达到$10^{11}\ \mathrm{GeV}$),贡献绝大部分有效剂量。一般在太阳活动极小时最大(还取决太阳磁性)。
GCR中还包含有所谓异常成分(anomalous component),星际间的中性粒子进入太阳系后,太阳辐射使其失去电子,离子太阳风作用和碰撞加速,其穿透地磁场的能力比其他成分更大,又可分为部分电离(singly-ionized anomalous component)和完全电离(fully-ionized anomalous component)。
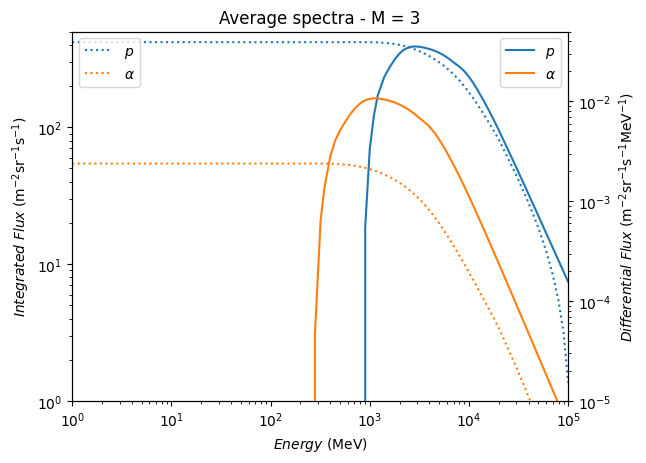
考虑异常部分,我们使用SPENVIS+CREME86模型进行模拟,获取1号(H)至28号(Ni)元素在$90%$最坏情况下的GCR通量(即实际情况大约只有$10%$的可能通量大于这一估计值,M=3)。
太阳辐射3
太阳辐射的主要来源是日冕抛射和太阳耀斑,具有明显的周期性,主要的周期有11年、22年等。太阳辐射以质子为主($90\sim95%$),通量可达$10^9\ \mathrm{cm^{-2}s^{−1}}$;其次为α粒子($5\sim8%$)。太阳活动较强时,质子的比例会上升。
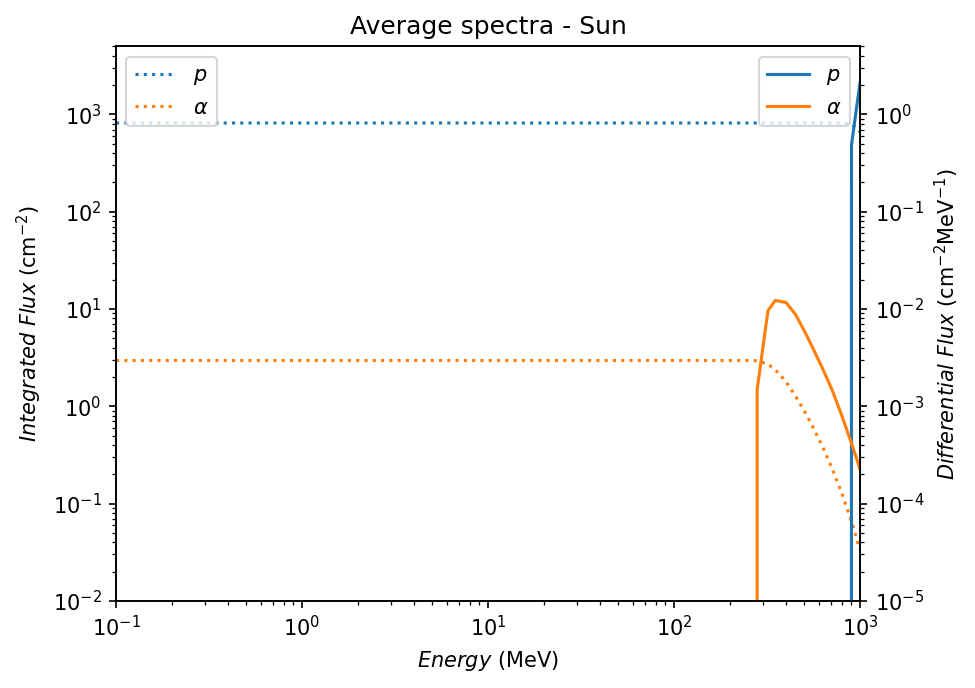
使用SPENVIS+SAPPHIRE模型太阳质子和太阳α粒子任务期间总通量,置信概率为$95%$(即实际情况大约只有$5%$的可能通量大于这一估计值)。
可以发现,整个任务期间的总通量不超过$10^3\ \mathrm{cm^{-2}}$,远远小于银河宇宙射线和俘获辐射带的通量,因此在后续模拟中忽略这一因素的剂量。
俘获辐射带3
近地俘获辐射带被称为Van Allen带,是部分宇宙射线、宇宙射线与地球磁场和大气层作用产生的带电粒子被地磁场俘获形成的辐射带,分为内外两个辐射带。
电子能量可达$7\ \mathrm{MeV}$,质子能量可达$600\ \mathrm{MeV}$,重带电粒子可达$50\ \mathrm{MeV/u}$,绝大部分是中低能量。
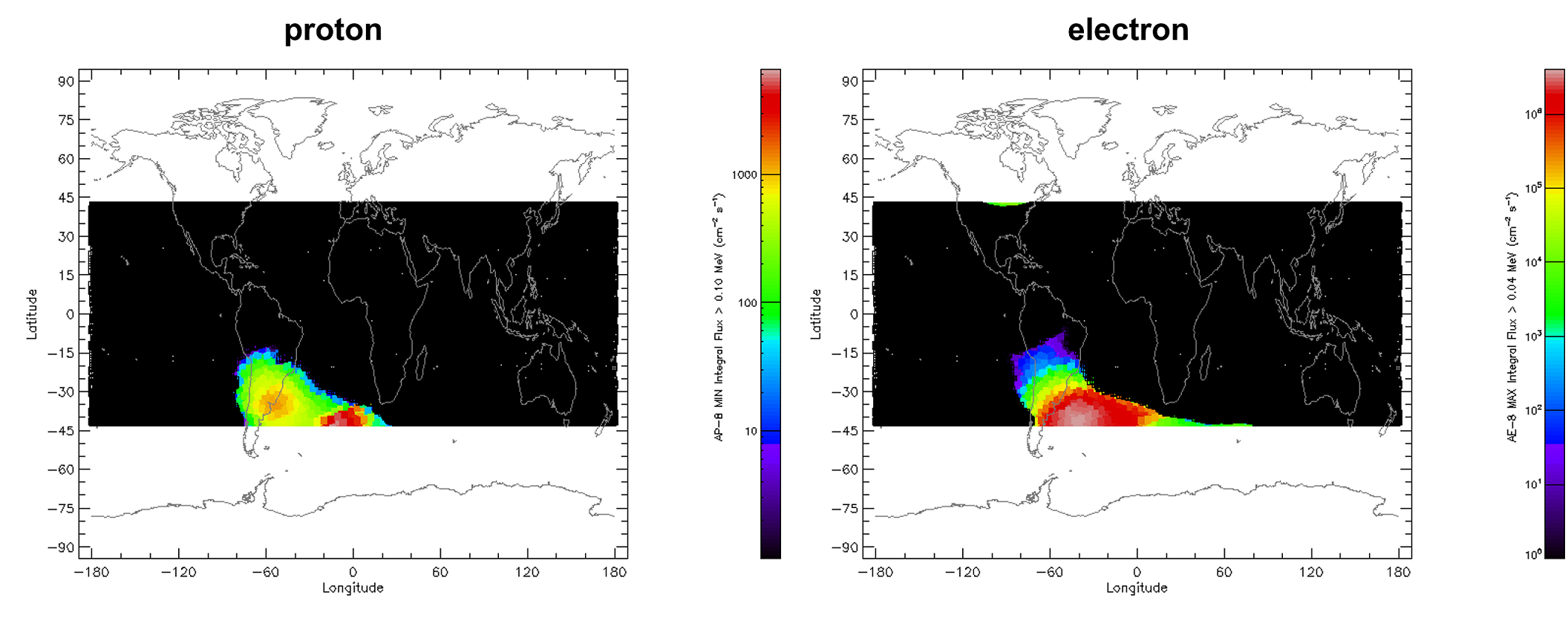
内带的高度一般在$600\ \mathrm{km}$以上,但是在高纬度地区和南大西洋地区,由于地磁异常,内袋高度会下降至$\sim300\ \mathrm{km}$,因此只有经过这些区域时才会有明显的俘获带电粒子通量。
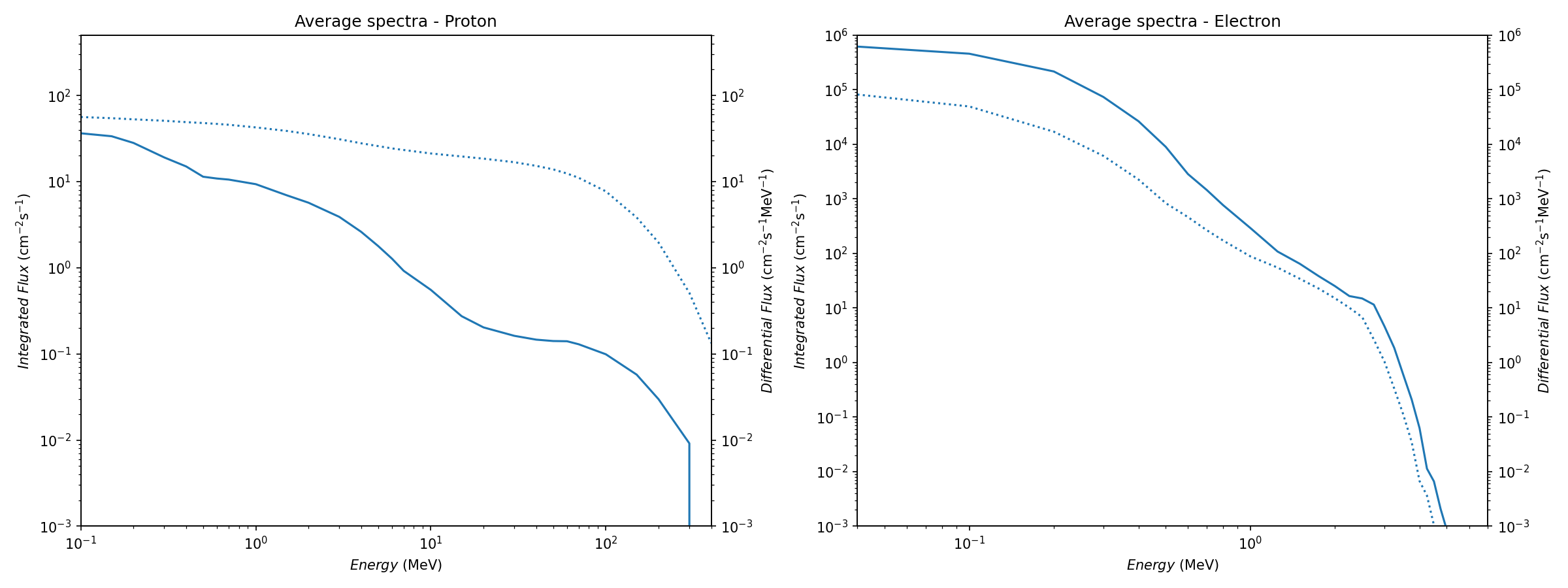
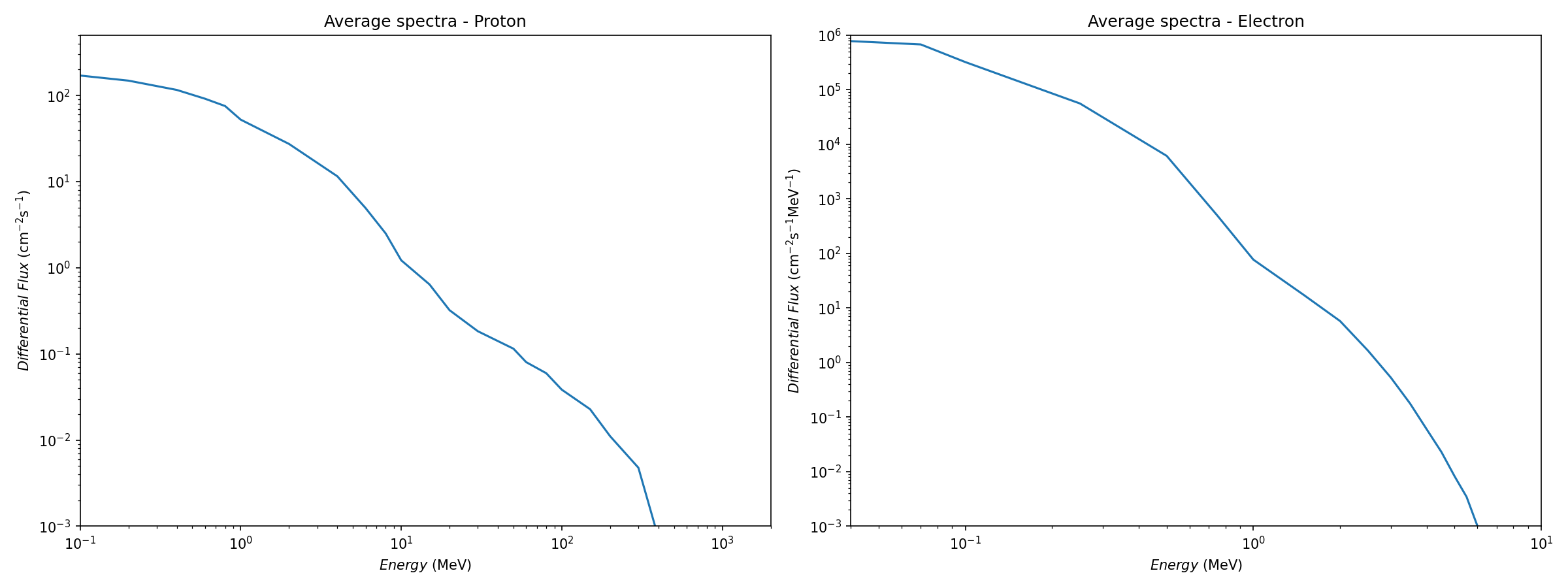
使用VDL的AE8/AP8模型,计算轨道上的太阳活动极大时的俘获质子通量和太阳活动极小时的俘获电子通量,对整个任务期间求均值,获得俘获质子/电子通量的能谱。同时使用AE9/AP9模型进行计算,通量略高于AE8/AP8模型。保险起见,采用AE9/AP9模型的结果。
辐射环境拟合
银河宇宙射线4
考虑GCR中1号(H)至28号(Ni)元素的强度模型,定义粒子刚度(particle rigidity)$R=\frac{pc}{Ze}$,其中$p$是粒子动量,$c$为光速,$Ze$是粒子电荷量,则有:
F(p,t) = \frac{C_i\beta^{\alpha_i}}{R(p)^{\gamma_i}}\left[\frac{R(p)}{R(p)+(0.37+3\times10^{-4}W(t)^{1.45})}\right]^{b\cdot W(t)+c}\frac{A_i}{Z_i}\frac{1}{\beta}
其中$pc=\sqrt{2m_0c^2E+E^2}$,不考虑$t$,则$W(t)$为常数,$C_i$,$\gamma_i$,$\alpha_i$为与粒子有关的常数,$A_i$,$Z_i$分别为质量数与电荷数,$\beta=\frac{v}{c}=\frac{pc}{\sqrt{m_0^2c^4+E^2}}$,则可简化为:
F(pc) = \frac{C_1\beta^{\alpha-1}}{pc}\left(\frac{pc}{pc+C_2}\right)^{C_3}
同时考虑简单的双指数模型:
F(E)=C_1e^{-C_2E}(1-e^{-C_3E+C_4})
两者同时进行拟合与比较,同时考虑简洁性,除H以外,其余元素均采用双指数模型,H采用简化模型。
俘获辐射带
-
电子5
在轨道较高($L>2.5$)的内带中,电子能谱中有$\sim64%$符合指数分布,$\sim4%$符合幂律分布。但在本例中,轨道较低($L\sim1.06$),因此使用指数模型$j = j_0e^{-\frac{E}{E_0}}$和幂律模型$j=j_0E^{-\alpha}$进行拟合,随后使用
Origin Lab对两者进行BIC test,最终选用指数模型$j_0=1.333680\times10^6,\ E_0=0.0824$。Model R^2BIC BIC diff Ex 0.98107 402.50208 0 Pow 0.94279 423.51296 21.01088 -
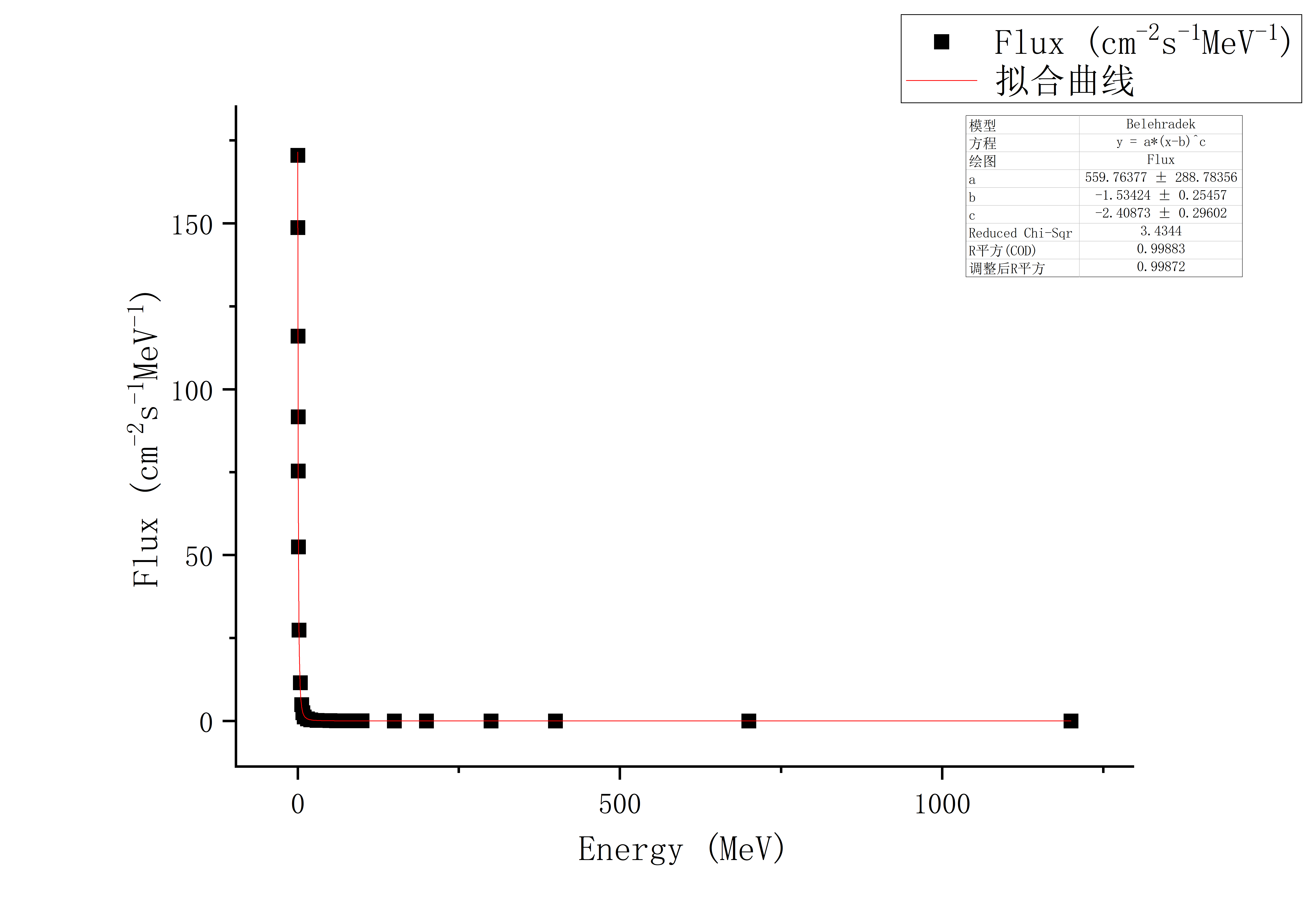
质子
与电子保持一致,幂律模型修改为$j=j_0(E-\beta)^{-\alpha}$,进行BIC test,最终选用幂律模型$j_0=559.76377,\ \alpha=2.40873,\ \beta=-1.53424$。Model R^2BIC BIC diff Ex 0.9957 67.24594 0 Pow-T 0.99883 39.11969 28.12625
辐射源设置
考虑在World球面上均匀随机发射粒子(各向同性),保证入射方向为球内,则球面上的计数率为:
F = A\int_{E_a}^{E_b} \phi(E)\mathrm{d}E,\ A=4\pi R^2
GCR的单位为$\mathrm{m^{-2}sr^{-1}s^{-1}}$,乘以$4\pi A$即可得到计数率;俘获辐射的单位为$\mathrm{cm^{-2}s^{-1}}$,乘以$A$即可得到计数率。经过检验,模型中使用的外壳(3层,2mm 铝 + 10mm 芳纶 + 5mm 铝)能够抵挡能量在$50\ \mathrm{MeV}$以下的质子和能量在$100\ \mathrm{keV}$以下的电子。
考虑到GCR和俘获辐射计数率相差太大,分为两部分分别进行模拟,同时按比例进行放缩,保证每一类粒子的模拟入射数目均不小于$10^5$。模拟得到剂量率后,乘以缩放系数和任务时长($30\ \mathrm{d}\times86400\ \mathrm{s/d}$),即可得到完整剂量。
| Partical | Model | R^2 |
E_{min}(\mathrm{MeV}) |
E_{max}(\mathrm{MeV}) |
Flux(\mathrm{s^{-1}}) |
Run | Zoom Factor |
|---|---|---|---|---|---|---|---|
e^{-} |
j=j_0e^{-\frac{E}{E_0}} |
0.98107 | 0.1 | 10 | 9.23242E+11 | 923242 | 999999.8096 |
p |
j=j_0(E-\beta)^{-\alpha} |
0.99883 | 50 | 1000 | 42853994.15 | 100000 | 428.5399415 |
H |
\frac{C_1\beta^{\alpha-1}}{pc}\left(\frac{pc}{pc+C_2}\right)^{C_3} |
0.98915 | 220 | 100000 | 12854310.92 | 100000 | 128.5431092 |
He |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.98936 | 220 | 100000 | 1720188.128 | 100000 | 17.20188128 |
Li |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99755 | 220 | 100000 | 12988.97006 | 100000 | 0.129889701 |
Be |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99708 | 220 | 100000 | 6691.176848 | 100000 | 0.066911768 |
B |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99569 | 220 | 100000 | 17105.83698 | 100000 | 0.17105837 |
C |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.98936 | 220 | 100000 | 52286.55444 | 100000 | 0.522865544 |
N |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.98892 | 220 | 100000 | 13576.5542 | 100000 | 0.135765542 |
O |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.98936 | 220 | 100000 | 48846.63508 | 100000 | 0.488466351 |
F |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99323 | 220 | 100000 | 1123.492483 | 100000 | 0.011234925 |
Ne |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99014 | 220 | 100000 | 8071.585382 | 100000 | 0.080715854 |
Na |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99263 | 220 | 100000 | 1866.8702 | 100000 | 0.018668702 |
Mg |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.98972 | 220 | 100000 | 10936.4597 | 100000 | 0.109364597 |
Al |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99217 | 220 | 100000 | 1940.381408 | 100000 | 0.019403814 |
Si |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.98873 | 220 | 100000 | 8269.257173 | 100000 | 0.082692572 |
P |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99183 | 220 | 100000 | 413.8897994 | 100000 | 0.004138898 |
S |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.98873 | 220 | 100000 | 1660.990128 | 100000 | 0.016609901 |
Cl |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99087 | 220 | 100000 | 372.0271181 | 100000 | 0.003720271 |
Ar |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99432 | 220 | 100000 | 751.7977189 | 100000 | 0.007517977 |
K |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.98963 | 220 | 100000 | 466.7118907 | 100000 | 0.004667119 |
Ca |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.98935 | 220 | 100000 | 1161.900661 | 100000 | 0.011619007 |
Sc |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99251 | 220 | 100000 | 231.5541271 | 100000 | 0.002315541 |
Ti |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.9934 | 220 | 100000 | 829.2810844 | 100000 | 0.008292811 |
V |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99424 | 220 | 100000 | 404.1724078 | 100000 | 0.004041724 |
Cr |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99313 | 220 | 100000 | 784.0902938 | 100000 | 0.007840903 |
Mn |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99385 | 220 | 100000 | 570.9732265 | 100000 | 0.005709732 |
Fe |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99351 | 220 | 100000 | 6028.059963 | 100000 | 0.0602806 |
Co |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99426 | 220 | 100000 | 20.90356212 | 100000 | 0.000209036 |
Ni |
C_1e^{-C_2E}(1-e^{-C_3E+C_4}) |
0.99231 | 220 | 100000 | 292.9961042 | 100000 | 0.002929961 |
由于模型较为复杂,且需要发射的粒子种类繁多,因此使用G4ParticleGun生成各类粒子,关键是生成各向同性(在球面上均匀分布)的位置、方向和符合能谱的能量分布。
-
Inverse Transform Method(ITM)
对于一个在$[a, b]$的分布,设其概率密度函数(PDF)为$F(x)$,对其积分可获得累积分布函数(CDF),记为$y=C(x)=\int_a^x F(u)\mathrm{d}u$,其反函数为$C^{-1}(y)$。设$y$为$[0, 1)$上均匀分布的随机数,则$x=C^{-1}(y)$满足$F(x)$的分布。 -
Acceptance-Rejection Method(ARM)
对于一个在$[a, b]$的分布,设其概率密度函数(PDF)为$F(x)$,首先生成一个均匀分布随机数$X \sim U(x_{min}, x_{max})$,随后独立生成另一个均匀分布随机数$Y \sim U(y_{min}, y_{max})$,如果$Y \le F(X)$,则保留$X$,保留下来的$X$满足$F(x)$的分布。
ITM也被称为反演法,关键是需要获取累积分布函数的逆函数,效率较高;ARM本质上是一种模拟算法,效率很低,但是适应性更广,特别是对于一些复杂分布函数。
-
位置生成
而发射位置要求在球面上均匀分布。由于球面的面积元$\mathrm{d}\Omega=\sin\theta\mathrm{d}\phi\mathrm{d}\theta$是$\theta$的函数,如果位置向量$\vec{r}(\rho, \phi, \theta)$的$\phi$和$\theta$是在$\phi\in[0, 2\pi)$和$\theta\in[0, \pi]$上均匀分布,选取的点将会在两极较为密集(即),因此可以采用ITM方法生成$\theta$:$C^{-1}(z)=\cos^{-1}(z)$。double u = rand(); double v = rand(); double phi = 2 * pi * u; double theta = arccos(2 * v - 1); double x = rho * sin(theta) * cos(phi); double y = rho * sin(theta) * sin(phi); double z = rho * cos(theta); -
发射方向6
在Geant4中,假定粒子的位置矢量为$\vec{r}$,则以$\vec{r}$反方向作为$z$轴正方向建立右手坐标系(简称为P系),随机生成指向$\vec{d}$,为了保证发射方向是朝向球面内,因此需要限制$\theta$的最大角度为$90^{\circ}$。double u = rand(); double v = rand(); double phi = 2 * pi * u; double theta = arccos(2 * v - 1); double x = sin(theta) * cos(phi); double y = sin(theta) * sin(phi); double z = cos(theta);
随后我们需要将$\vec{d}$转化到World坐标系(简称为W系)中,已知两个坐标系有两个公共点,在W系中表示为原点$O$和发射点$\vec{r}=(x_0,y_0,z_0)$,在P系中则为$(0,0,\rho)$和原点O^\prime,则有:
\begin{bmatrix}
x\\\ y\\\ z
\end{bmatrix} = \lambda R \begin{bmatrix}
u\\\ v\\\ w
\end{bmatrix} + \begin{bmatrix}
x_0\\\ y_0\\\ z_0
\end{bmatrix}
\cdots(1)
其中$\lambda$为尺度比例因子,设置为1;$R$被称为罗德里格矩阵,定义反对称矩阵:
S = \begin{bmatrix}
0,& -c,& -b \\\
c,& 0,& -a \\\
b,& a,& 0
\end{bmatrix}
则$R$可表示为$R = (I+S)(I-S)^{-1}$,展开后则有:
R = \frac{1}{1+a^2+b^2+c^2}\begin{bmatrix}
1 + a^2 - b^2 - c^2, -2c - 2ab, -2b + 2ac \\\
2c - 2ab, 1 - a^2 + b^2 - c^2, -2a - 2bc \\\
2b + 2ac, 2a - 2bc, 1 - a^2 - b^2 + c^2
\end{bmatrix}\cdots(2)
将两个公共点代入$(1)$,相减则可消去平移项,可得到:
\begin{bmatrix}
x_2-x_1\\\ y_2-y_1\\\ z_2-z_1
\end{bmatrix} = R \begin{bmatrix}
u_2-u_1\\\ v_2-v_1\\\ w_2-w_1
\end{bmatrix}
代入$(2)$则可得到($u_{21}=u_2-u_1$):
\begin{bmatrix}
0,& w_{21}+z_{21},& v_{21}+y_{21} \\\
w_{21}+z_{21},& 0,& -u_{21}-x_{21} \\\
-v_{21}-y_{21},& -u_{21}-x_{21},& 0
\end{bmatrix}\begin{bmatrix}
a\\\ b\\\ c
\end{bmatrix} = \begin{bmatrix}
u_{21} - x_{21} \\\
v_{21} - y_{21} \\\
w_{21} - z_{21}
\end{bmatrix}
代入本题,则有:
\begin{bmatrix}
0,& -\rho+z_0,& y_0 \\\
-\rho+z_0,& 0,& -x_0 \\\
-y_0,& -x_0,& 0
\end{bmatrix}\begin{bmatrix}
a\\\ b\\\ c
\end{bmatrix} = \begin{bmatrix}
-x_0 \\\
-y_0 \\\
-\rho-z_0
\end{bmatrix}
令$a=1$,则可求得:
\begin{cases}
b = \frac{z_0+\rho-y_0}{x_0} \\\
c = \frac{z_0-\rho+y_0}{x_0}
\end{cases}
计算得到$R$,继而根据$(1)$计算得到$\vec{d}$在W系中的表达式(最终无需平移,即不需要$+\begin{bmatrix}x_0\\ y_0\\ z_0\end{bmatrix}$)。
- 能量
-
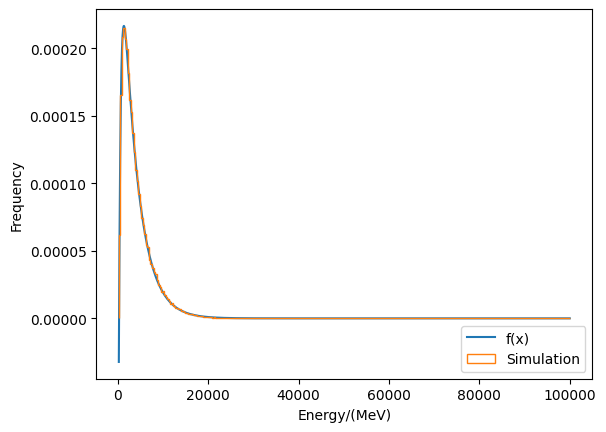
俘获电子的函数较为简单,采用
ITM;(下表中$j_0$已经归一化)F(E)\int F(E)\mathrm{d}EC(x)=\int_a^xF(u)\mathrm{d}uC^{-1}(y)j=j_0e^{-E/E_0}-j_0E_0e^{-E/E_0}j_0E_0e^{-a/E_0}-j_0E_0e^{-x/E_0}-E_0\ln(\frac{C-y}{j_0E_0}),\ C=j_0E_0e^{-a/E_0} -
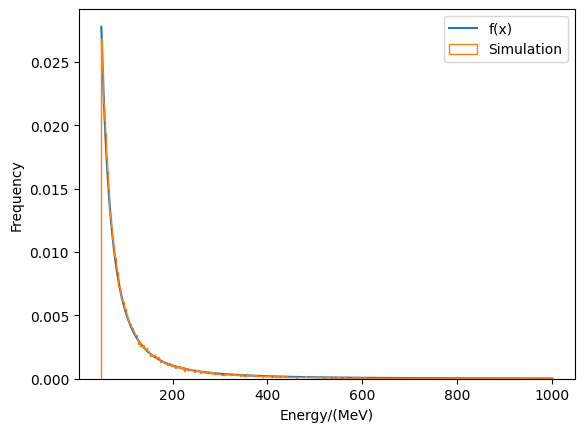
俘获质子的函数较为简单,采用
ITM;(下表中$j_0$已经归一化)F(E)\int F(E)\mathrm{d}EC(x)=\int_a^xF(u)\mathrm{d}uC^{-1}(y)j=j_0(E-\beta)^{-\alpha}\frac{j_0(E-\beta)^{1-\alpha}}{1-\alpha}\frac{j_0}{1-\alpha}\left((x-\beta)^{1-\alpha}-(a-\beta)^{1-\alpha}\right)\sqrt[1-\alpha]{\frac{(y+C)(1-\alpha)}{j_0}}+\beta,\ C=\frac{j_0(a-\beta)^{1-\alpha}}{1-\alpha} -
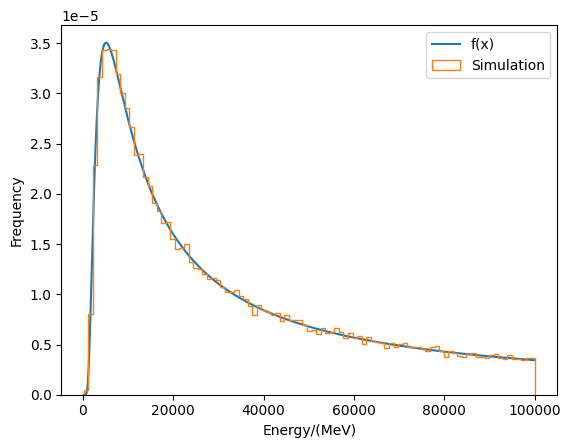
GCR质子的函数较为复杂,使用ARM生成100000个随机数需要12分钟,效率满足要求; -
其余
GCR辐射粒子同样使用ARM,生成100000个随机数需要4.5分钟。
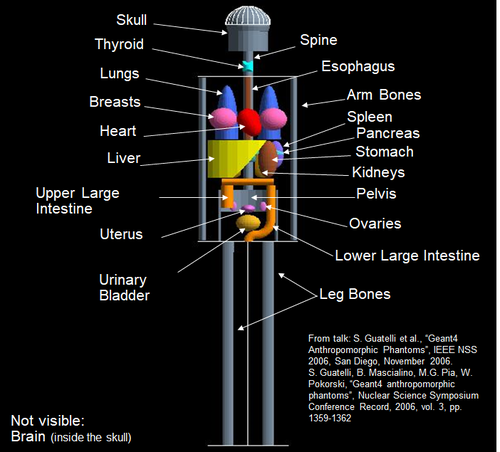
体模
使用Geant4示例中的MIRD人体模型,分为男、女两个性别,
空间站建模
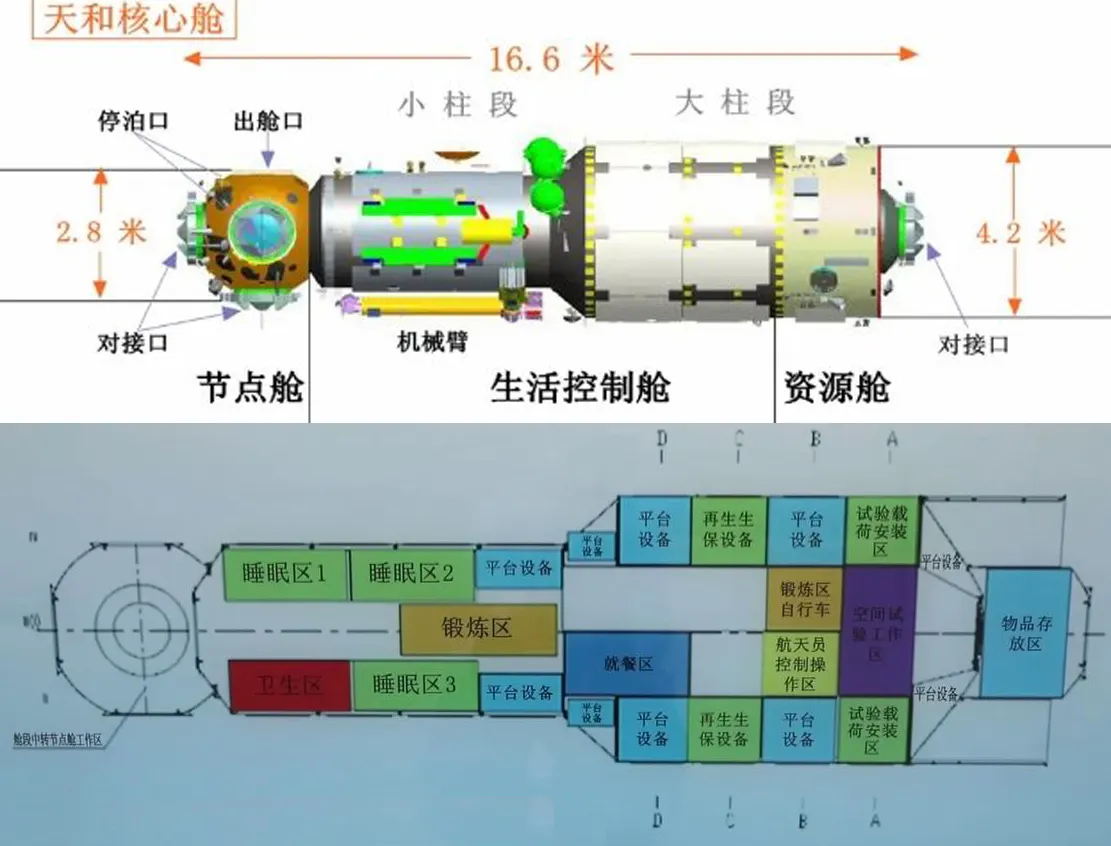
- 尺寸与分区7
- 全长:16.6 m
- 总重:22.5 t
- 体积:143.6
\mathrm{m^3} - 分区:
- 大柱段
- 外径:4.2 m
- 长度:4.32 + 2.40 m (生活控制舱 + 资源舱)(直线过渡)
- 过渡段:0.815 m
- 小柱端
- 外径:2.8 m
- 长度:5.18 m
- 过渡段:0.33 m
- 节点舱:以直径 2.8 m 的球体近似
- 大柱段
- 材料
- 特别区域
睡眠区无填充,仅考虑加厚外壳为 3层 5mm 铝 + 15mm 芳纶 + 10mm 铝
待改进
- 建模
- 体模
- 空间站模型
- 材料
- 大小
- 辐射环境
- 太阳活动极大时
- 太阳活动极小时
- 更长的任务尺度
- 各向异性的模拟(如俘获辐射带质子各向异性通量)
- 太阳质子的检验
-
程彭超,闵锐.近地空间辐射环境与防护方法概述[J].辐射防护通讯,2017,37(01):14-21. ↩︎
-
Bourdarie S, Xapsos M. The near-earth space radiation environment[J]. IEEE transactions on nuclear science, 2008, 55(4): 1810-1832. ↩︎
-
Matthiä D, Berger T, Mrigakshi A I, et al. A ready-to-use galactic cosmic ray model[J]. Advances in Space Research, 2013, 51(3): 329-338. ↩︎
-
Zhao H, Johnston W R, Baker D N, et al. Characterization and evolution of radiation belt electron energy spectra based on the Van Allen Probes measurements[J]. Journal of Geophysical Research: Space Physics, 2019, 124(6): 4217-4232. ↩︎